FAQ

How to get access?

  • Which access options exist?

    There are two main access options: access through a web interface / GUI and access through an API. Web interface / GUI access comes in two forms: Either you get your personal email address registered (not possible anymore) or you have your university library subscribe to our service and you can use your university email address to access our calculators.

    Besides these options to access our full capabilities, there is the option to use the basic abnormal return calculator with results prompt directly on the website.
     
  • How can I integrate the EST API into my own program?

    Application Programmable Interfaces (APIs) have become the standard for inter-program communication. EventStudyTools offers its capabilities not only through a graphical user interface (GUI) or an R-package but also through direct API calls.

    To integrate our API into your software, please follow our integration guide. Besides placing the correct calls and providing the needed input data files, you will need a valid API key.

 

How to Use EST ARC?

  • How does EST work, in short?

    Event studies are complex and developing their algorithms is even more so. EventStudyTools was built to make your research life easier. Our research apps perform all calculations needed for large-scale event studies. While we have multiple apps for different purposes (e.g., for volume event studies or news analytics), the Abnormal Return Calculator (ARC) is most likely the research app that brought you here. In a nutshell:

    • ARC requires you to upload three input data files. Thereafter, it calculates all abnormal returns, test statistics, and p-values
    • You can use ARC through a graphical user interface (GUI) or our R-package. Most users choose the GUI. You find it here, it looks as follows:

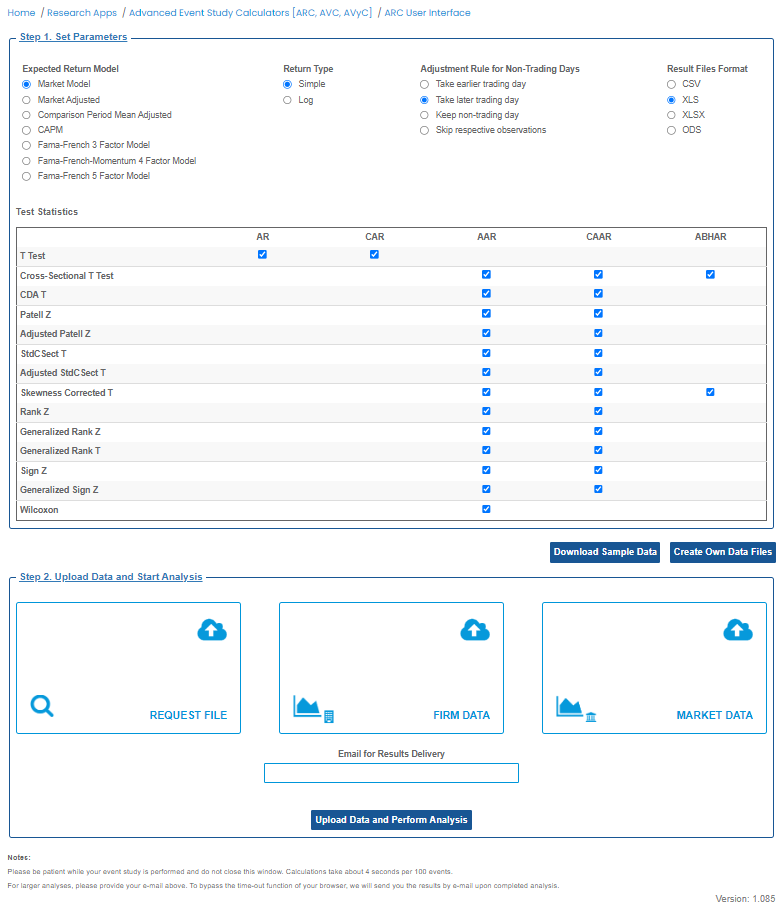
      The upper part of the interface lets you choose broad parameters of your event study. The mid-section informs you about the test statistics that will be produced at the different levels of analysis. The lower data upload section lets you upload your input files.Creating your three input files is the most challenging part of the whole process. Please first download the sample data and review it in a text editor. Try to understand the data structure with the help of the introduction page. We added a link to the sample data also on the GUI page. 

      Once you created your input files, you can lay back and let ARC do the rest of the work. It processes your input data and sends your event study results to your e-mail address. Also, it prompts the results on the GUI in case you can't access your emails.

      If you would like a more comprehensive introduction, please read our article on Medium—or have it read aloud to you by Medium.
       
  • How shall I build my ARC input files?

    To function properly, the abnormal return calculator (ARC) requires input files in a certain structure. The required structure is described on this instruction page and illustrated by sample input files.

    We strongly recommend viewing these sample files with a text editor - this will show you the target structure and variable formats (e.g., the date format or the need to use a dot as the decimal separator). Viewing the files in spreadsheet software (e.g., Excel) is not recommended since spreadsheet programs interpret the data and may display for example the dates in your country scheme.

    If you want to have the firm and market data files created for you, based on your request file, consider using our input data file creation service.

  • What are the most common bugs in ARC input files and how to fix them?

    We work on making our research apps as robust and error-tolerant as possible. Yet, some bugs in input data will always require the intervention of the user. For example, our apps can not fill data gaps. On this page, we list the most common bugs, provide illustrative screenshots, and explain how to fix the files.

    Before looking at the most common bugs, let's first have a look at what your files should look like. See screenshots of the sample data below, opened in a text editor, such as Microsoft Window's NotePad:

    01_RequestFile
    02_FirmData 03_MarketData

    If you open your input files in the text editor and they look different, the abnormal return calculators will likely not perform the analysis and display an error message that guides you to the first error the app encounters when loading the data.

    It is crucial that you use identical syntax for the firm and index names across all three files. The Request File steers the analysis and then links the data from the other two files. If you use mismatching syntax, the data will not be merged as required for the analysis.

    Further, please note that some errors do not fail the overall analysis (e.g., misspecified event windows) but lead to skipped events/instances. You find these cases listed in the "overarching comment"-section of the Analysis Report file.

    The Most Common Bugs:

    #1 Bug: Commas used instead of semicolons as column separators

    Example of the bug:

    Why this issue arises: 

    Excel or any other spreadsheet software typically inherits a local scheme for separators and date formats from your system settings.

    When you store your file in CSV format, the spreadsheet software may place commas (e.g., in Germany).

    EST ARC requires semicolons because commas are also often part of company names or are also used as a decimal separator.

    The fix: Use your text editor's function to replace all commas with semicolons. 

    #2 Bug: Wrong date formats

    Example of the bug:

    Why this issue arises: 

    Wrong date formats are a common error, for two main reasons: First, date conventions vary across countries, and spreadsheet software thus saves according to the local schemes. Second, sometimes dates are not recognized correctly in the spreadsheet program - when then stored as CSV, the date gets recorded as a number (see the third example in the picture on the left).

    EST ARC allows two date formats: DD.MM.YYYY and YYYY-MM-DD.

    The fix: There are two options if you have the wrong local scheme. Either change the local date scheme in your spreadsheet program or create the date string not as format date but as format text - for this, if you use Excel, use the formula concat().

    #3 Bug: Duplicate data in firm or market files

    Example of the bug:
    or

    Why this issue arises: 

    This issue may arise when you combine multiple data time series of one index or firm - which may be needed if you have multiple events of the same firm/index in your sample.

    EST does not allow for duplicate data since it cannot decide which of the entries should be the right one.

    A duplicate is two lines of one index/firm and date combination - with the same or different prices (see screenshots on the left). Both cases will corrupt ARC.

    The fix: For fixing this bug, you will need your spreadsheet software. In MS Excel, for example, you can mark the data (company/index name and date) in your input files and select the function "delete duplicates". Please note that for a single company or index, there cannot be more than one closing price in one day.

    #4 Data Gaps: Missing data that cannot be filled

    Example of the bug:

    or

     

    Why this issue arises: 

    The data from your data provider may have gaps.

    The first example on the left shows the Market Data file for the Fama-French 5-Factor Model of a recent user. Instead of closing prices, it holds the text value "NULL" in several instances within the price vector. 

    The second example on the left was fabricated using the Firm Data file from our sample dataset. 

    ARC cannot interpret text inputs where it expects numbers, nor can it fill gaps of data. It will prompt you a corresponding error message.

    Data bugs for which our import mechanism now automatically corrects:

    Random commas or semicolons at the end of your input file

    Example of the bug:

    Why this issue arises: 

    When editing data in Excel or any other spreadsheet software, one regularly copies around whole columns and deletes some. 

    When you then store your file in CSV format, the spreadsheet software often keeps those deleted/empty columns in your file.

    EST ARC then finds more than the required 3 columns in the input files and has issues with reading your inputs.

    The fix: Use your text editor's function and replace all occurrences of multiple commas or semicolons next to each other with nil/nothing - this factually deletes all unneeded commas/semicolons. Since there is no find & delete in most editors, you need to find & replace.

  • How to create sub-samples with the grouping variable?

    Published event studies often differentiate between event types. For example, M&A research may differ between acquisitions and mergers, while accounting research may differ between positive and negative earning statements.

    Such differentiation does not mean you have to run multiple event studies. With the EST Abnormal Return Calculator (ARC), you have the option to assign the events in your request file to groups - using the grouping variable.

    The grouping variable then stratifies your overall set of events and calculates separate AAR- and CAAR-level results for these groups. This comes in handy since it saves you the time of re-running analyses for each group.

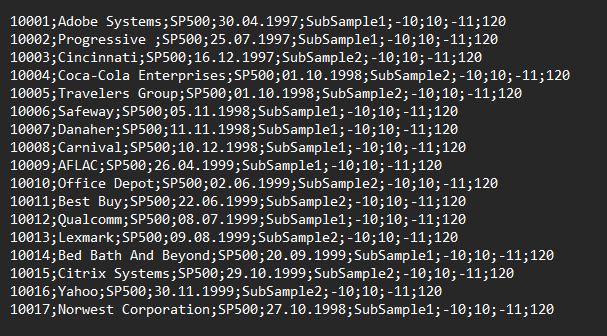
    Looking at the example request file provided on our website, you can see how the grouping variable is applied:

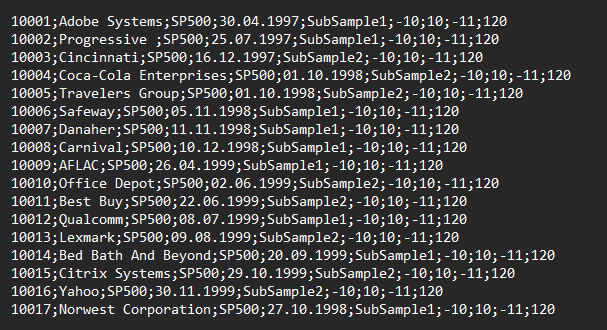
    In the fifth column of the CSV file structure, you can place any texts to describe your subgroups. In the example shown, two subgroups will be created: "SubSample1" and "SubSample2". When you apply it, please use words that are closer to your studied event types.

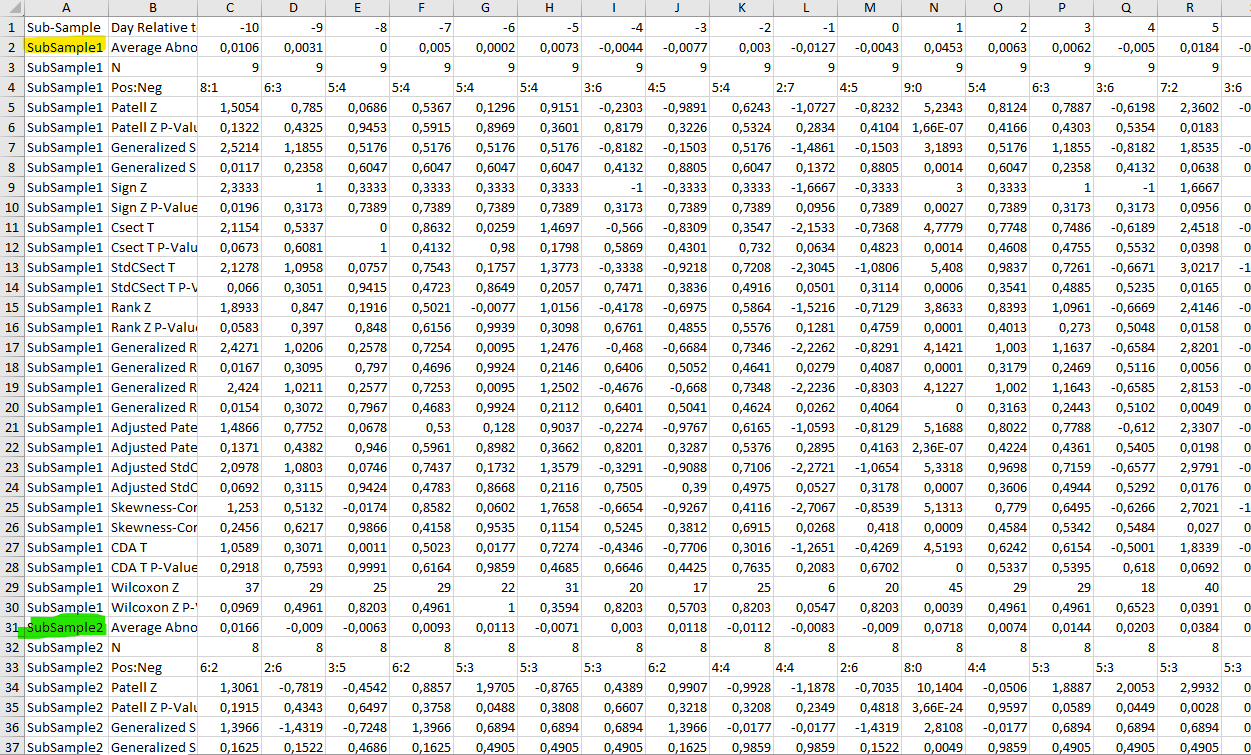
    The AAR- and CAAR-result files both start with a column that indicates to which sub-sample the presented abnormal returns and test statistics belong. See below the example of the AAR-level results as it gets produced for the EST standard example input file set.

  • Why should I auto-adjust for non-trading days?

    Event studies capture the effects of events on stocks. These price, volume, and volatility effects arise from new information that is disseminated to and processed by the capital markets. Capital Markets, however, do have trading hours and do not operate on public holidays. Thus, in case an event took place on a non-trading day, an adjustment is needed. Typically, the right choice is to auto-adjust to the later date - unless there is a strong reason to assume the information was processed by the capital markets on the day before of the event.

 

How to Best Choose Event Study Parameters?

  • What is the estimation window and how long should it be?

    The estimation window lies earlier in time than the event window. It serves one purpose: to inform the expected return models about the typical relationship between the analyzed company and its reference index. It does so by performing a regression on the company stock's returns with the market (or other factors) returns as the independent variable(s).

    For the identified relationship to be robust, the estimation window needs to be of sufficient length. Most event studies use estimation windows of at least 80 trading days. Our recommendation is to use 120. For a more extensive discussion of this topic, visit our page on the methodological blueprint of event studies.

    The estimation window should not overlap with the event window. For this reason, we recommend using a gap / pointer to the end of the estimation window that is greater than the distance between the event date and the beginning of the event window - see the below graphic and the example underneath. 

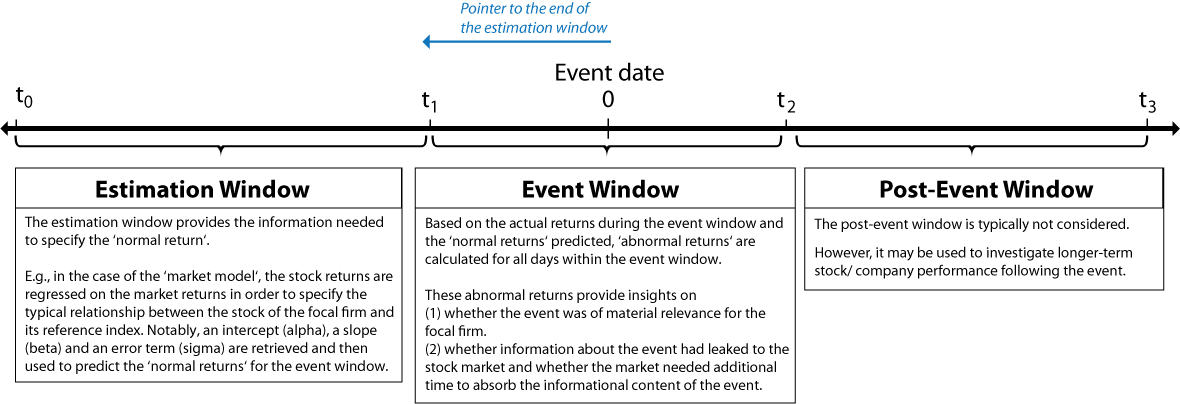
    For example, in case your event window is (-5,5), you should choose a pointer of at least -5. If informational leakage of the event is possible, pick a larger negative number, such as -10.

    As you design your empirical analysis, you will write a request file with all the parameters you want to apply. You see an example request file below. For each line (i.e., event that you study), you specify the company affected, its reference index, the event date, and so forth. The last two parameters you provide are about the estimation window. In the below example, the "pointer to the end of the estimation window" is set to -11 (i.e., 11 trading days prior to the event), and the length of the window is set to 120 trading days.

    The estimation window and its positioning relative to the event data have the following implication for your firm and market data files: They jointly define the time series of data you need to provide prior to the event. Note that the data you need to provide after your event depends on the event window.

    In case you choose the above parameters of -11 and 120 for the pointer and the estimation window length, you will need your financial data on the firm and the reference index to cover this period. Assuming your event window starts right thereafter, you would need 131 returns prior to the event, which equates into 132 closing prices (or trading dates). In terms of calendar days, this easily translates then into 160 or more days given weekends and other non-trading days, such as public holidays.

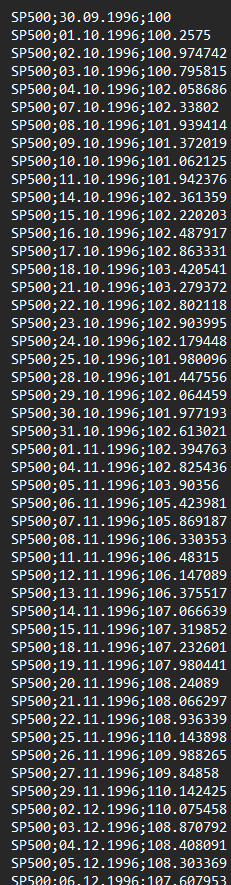
    Please see below a screenshot of the input files from the sample data set. The point you should notice is that the market data file must cover the joint time ranges of your firms from the firm data file.

    Firm Data File Market Data File

 

How to Interpret Test Statistics?

  • What is the difference between a parametric and a non-parametric test statistic?

    A parametric test assumes that data follow a certain parametric distribution, with the most common assumption being that of a normal distribution. Strictly speaking, if the assumption is violated (e.g., if the data do not follow a normal distribution), then the test is no longer (exactly) valid. But most parametric tests, and all of the parametric tests employed by us, are robust in the sense that if the sample is large, then the test is still valid `in practice' in the sense that, although is not exact, it will deliver a very good approximation. There is no hard-and-fast rule saying when the sample size is large (enough), but as a rule of thumb 30 to 50 generally does. What constitutes the sample depends on the application. For example, when testing AAR or CAAR, the sample refers to the number of firms included. So if one only has five or ten firms in the sample, then a parametric test is actually not a good idea.

    A nonparametric test, on the other hand, does not make any assumption about the data following a certain parametric distribution. They can therefore also safely employed when the sample size is small. Of course, they also work well when the sample size is large. 

    In practice, parametric tests are still more popular than nonparametric tests for historical reasons (as they often were developed first) and then because people tend to do "as others have done in past". We feel that, if anything, nonparametric should be(come) more popular and that's why we have several of them on our menu!

  • What is a p-value?

    The p-value is defined as the probability of obtaining a test statistic at least 'as extreme' as the value observed for the data at hand under the assumption that the null hypothesis is correct. (Recall, in EST's test statistics, the null hypothesis is that AR, CAR, AAR, or CAAR are equal to 0.)

    Arguably, this definition is not easy to understand for users not versed in statistical theory and, over the years, has created lots of confusion. So we propose to instead focus on what a p-value essentially means: the amount of evidence contained in the data against the null hypothesis or, equivalently, in favor of the alternative hypothesis. A p-value is a number between zero and one and the smaller the number, the stronger the evidence. Common cut-off values are as follows: a p-value less than 0.1 means `somewhat of evidence', a p-value less than 0.05 means `solid evidence', and a p-values less than 0.01 means `very strong evidence'. Most researchers use the cut-off of 0.05 to determine whether there is evidence or not.

    There is an important asymmetry that is missed by many users and even quite a few academic researchers: Whereas a small p-value constitutes evidence in favor of the alternative hypothesis, a large p-value (say a p-value of 0.6) does not constitute evidence in favor of the null hypothesis. In other words, a small p-value `proves' (beyond a reasonable doubt) that the alternative hypothesis is true whereas a large p-valued does not `prove' that the null hypothesis is true. All one can say in the latter case is that the null hypothesis is `plausible' or `not rejected' by the data.

    An analogy might help to understand this asymmetry (better): a court case. In a court case, the null hypothesis plays the role of "the defendant is innocent" and the alternative hypothesis plays the role of "the defendant is guilty". During the court case, one looks at "data" in order to determine which hypothesis to go with in terms of the verdict. If there is strong evidence against the null, say in form of trustworthy testimony or crime-scene analysis, one arrives at the verdict of "guilty" and the defendant is sentenced. In this case, the guilt (that is, the alternative) is considered proven (beyond a reasonable doubt). On the other hand, in the absence of such evidence, one arrives at the verdict of "innocent" and the defendant is set free. But in this case, innocence is not necessarily considered proven. Perhaps there was some evidence but just not enough to arrive at a guilty verdict. So then if the defendant is set free (that is, one goes with the null hypothesis) one is not necessarily convinced of his/her innocence; a leading example is the O.J. Simpson murder case trial. Of course, there may be cases where an innocent verdict may go along with proven innocence (beyond a reasonable doubt), say if a trustworthy alibi can be produced; but such cases are not universal.

  • What is the difference between a T score and a Z score?

    This has to do with the (approximate) distribution of the test statistic under the null hypothesis. This distribution, together with the value of the test statistic, is used to compute the p-value, which is all the user of the test needs eventually. If the (approximate) distribution of the test statistic under the null hypothesis is a t-distribution (with a certain degree of freedom), then the test statistic is called a T score; on the other hand, if it is standard normal, then the test statistics is called a Z Score.

    In the end, this information can be considered "nice to have" but it does not have any practical bearing. All that matters to the user is the p-value. How it was obtained is of interest to the statistician, to the user, it is "under the hood" stuff.

  • Which test statistic should I choose?

    It's hard to answer this question in detail in all generality. But we can at least give some high-level pointers here.
    First of all, everything depends on the parameter you want to test, that is, AR, AAR, CAR, or CAAR. It is paramount to use a test statistic in the relevant category. As an analogy, the best method to cook a steak will yield unsatisfactory results if you are in the mood for pizza or sushi.

    Within any category, we offer a sub-menu of test statistics. The main distinction here is between parametric and nonparametric tests, which is addressed in a separate question. in a nutshell, if the sample is small, a nonparametric test is always preferred, but even for large(r) sample sizes, nonparametric tests are not necessarily worse, although they (still) tend to be less used than parametric tests.

    Last but not least, for any test to be valid (or trustworthy) a certain list of assumptions needs to be fulfilled. As an analogy, if you want to cook a certain recipe, you need to make sure that you have the proper ingredients and cooking equipment at hand; the best recipe for cooking a steak will fail if your main ingredient is a shoe sole instead. To learn more about this important topic, see the separate article "Which assumptions do the various test statistics make?".

  • What assumptions do the various test statistics make?
    Overview of the test statistics EST calculates

    Test statistic Applicability Type
    T-Test AR, CAR Parametric
    CSect T AAR, CAAR Parametric
    Skewness Corrected T AAR, CAAR Parametric
    CDA T AAR, CAAR Parametric
    Patell Z AAR, CAAR Parametric
    Adjusted Patell Z AAR, CAAR Parametric
    StdCSect T AAR, CAAR Parametric
    Adjusted StdCSect T AAR, CAAR Parametric
    Rank Z AAR, CAAR Non-parametric
    Generalized Rank Z AAR, CAAR Non-parametric
    Generalized Rank T AAR, CAAR Non-parametric
    Sign Z AAR, CAAR Non-parametric
    Generalized Sign Z AAR, CAAR Non-parametric
    Wilcoxon AAR Non-parametric

    Every test statistic is based on a list of assumptions, which ensure that the corresponding p-value can be trusted in practice.

    For the technically inclined user: The p-value is based on the (approximate) distribution of the test statistic under the null hypothesis, and in order to derive this distribution certain assumptions are needed in each case.

    Parametric test statistics

    Test statistic Assumptions
    T-Test

    The abnormal returns AR, over both the estimation window and the event window, are independent and identically distributed (i.i.d.) according to a normal distribution with mean zero and unknown (but common) variance. 

    CSect T

    Across the N stocks, the abnormal returns AR are independent and identically distributed (i.i.d.) according to a normal distribution with mean zero and unknown (but common) variance. Note that this variance may differ from the variance(s) of the abnormal returns during the estimation window so that the test is robust to event-induced increases in variance(s). 

    Skewness Corrected T

    Same as in CSect T except that the common distribution does not have to be normal, and thus may exhibit skewness. 
    CDA T

    The average abnormal returns AAR, over both the estimation window and the event window, are independent and identically distributed (i.i.d.) according to a normal distribution with mean zero and unknown (but common) variance. This allows for the abnormal returns AR to have (i) cross-sectional dependence on any given day and (ii) different variances across stocks. However, the test is not robust to event-induced increases in the variance of the average abnormal returns AAR. 
    Patell Z

    Across stocks, the standardized abnormal returns SAR (for testing AAR), respectively the cumulative standardized abnormal returns CSAR (for testing CAAR), are independent and identically distributed according to a normal distribution with mean zero and unknown variance, which is the same as the variance during the estimation period. Hence, this test is not robust to event-induced increase in variance(s). 
    Adjusted
    Patell Z

    Same as for Patell Z except that the abnormal returns AR are allowed to be correlated across stocks on any given day. The pairwise correlations are assumed to be constant through time and to be identical to their counterparts during the estimation window (which are also constant through time). 
    StdCSect T

    Same as for Patell Z except that for a given stock the variance of the (standardized) abnormal return for t = 0 can be different compared to the estimation window. Hence, this test is robust to event-induced increase in variance(s). 
    Adjusted StdCSect T Same as for StdCSect T except that the abnormal returns AR are allowed to be correlated across stocks at any given day. The pairwise correlations are assumed to be constant through time and to be identical to their counterparts during the estimation window (which are also constant through time). 

    Apart from Skewness Corrected T, all parametric test statistics assume that the stock returns follow a normal distribution. This assumption is hard to check in practice and does not hold for most stocks. The good news is that a violation of the normality assumptions does not matter (much), in the sense that the resulting p-values can still be trusted, as long as the relevant sample size is sufficiently large; with the exception of the T-test, "relevant sample size" means the number stocks always. There is no hard-and-fast rule as to what constitutes "sufficiently large" in practice but, as a rule of thumb, a sample size greater than 50 is typically enough, and even a sample size greater than 30 can suffice. Consequently, if the number of stocks is less than 30, we recommend not using parametric test statistics and, instead, switching to non-parametric test statistics. For the T-Test, the "relevant" sample size means the number of days in the event window; unless this number exceeds 30, we recommend not to use this test. (In particular, we recommend not to use this test for testing AR, since in this case, the number of days in the event window is only one.)

    Non-parametric test statistics

    Test statistic Assumptions
    Rank Z For any given stock, the full sequence of abnormal returns AR, covering both the estimation and the event window, are i.i.d. according to an arbitrary distribution which need not be normal. Across stocks, the distributions may differ, allowing for different
    variances, say. However, the assumptions do not allow for an event-induced increase in variance(s).
    Generalized Rank Z Strictly speaking, same as Rank Z. However, this test works with standardized abnormal returns SAR instead of `simple' abnormal returns AR and is in practice more robust to event-induced increase in variance(s). Furthermore, Monte Carlo studies have shown that this test is also robust to mild serial correlations in returns, which can arise for some stocks. 
    Generalized Rank T Same as Generalized Rank Z. But, in addition, Monte Carlo studies have shown that this test is (more) robust to cross-sectional dependence of stock returns. Therefore, this is the preferred Rank test of the three, for testing both AAR and CAAR.
    Sign Z

    For testing AAR, across stocks, the abnormal returns AR on the event day are independent and have the same probability p to be greater than zero; under the null p = 0.5. For testing CAAR, it's analogous to "CAR during the event window" in place of "AR on the event day".
    Generalized Sign Z Same as Sign Z but the probability p under the null need not be equal to 0.5 and is estimated from the estimation window. (This is a useful generalization since if the distribution is skewed it can have a mean of zero but the probability of getting a number greater than zero must not be equal to 0.5 at the same time.)
    Wilcoxon The sample of abnormal returns AR, across stocks, is i.i.d. and the probability of observing a positive AR under the null is 0.5. Therefore, this test is not robust to skewed distributions that have a mean of zero but a probability different from 0.5 resulting in a positive AR (under the null).

    Unlike parametric tests, nonparametric tests do not rely on normality assumptions on the stock returns and, therefore, can also safely be used for small(er) sample sizes. Although, for the sake of completeness, we have several nonparametric tests in our menu, at the end of the day the recommendation from our side is quite simple: Use the Generalized Rank T test for testing both AAR and CAAR; it's "the latest and the best" of the tests in the menu. (Compared to other tests it is more complicated to code and implement, but this is of no concern to the user, since we have done the job for you.)

  • How do I interpret test statistics?
    The short answer: You don't have to.

    The longer answer: The test statistic, together with its (approximate) distribution under the null hypothesis are "means to the end" of computing the p-value, which is all the user needs eventually to understand the outcome (or the decision) of a test.

    The value of the test statistic itself is provided as a "bonus" to those users more versed in statistical methodology, and who would like to see it in addition to the p-value. But it does not add any real (further) value, pun intended.

Other questions

  • Have EST-ARC results been validated?

    We are certain that our ARC's results are correct. Why? For two reasons: First, our algorithms and the inherent test statistics are coded by a renowned statistics professor. Second, we validate our results by benchmarking them against alternative software solutions and published research papers.

    For different variables/results (e.g., individual test statistics), there are different pieces of evidence - from differing sources. For example, the abnormal returns at AR- and CAR-levels can be verified against an Excel calculation, whereas the test statistics can only be compared against alternative event study software solutions and published research papers. We constantly expand our validation and search for papers (incl. data) or alternative software that contain or produce benchmark values for the few variables/results that have not been able to validate yet. 

    Fortunately, we have been able to benchmark most of our statistical results as of today already. The tables below provide an overview of the current state of validation of EventStudyTools' (EST) outputs.

    Test statistics can only match their benchmark values if also the underlying abnormal returns match. We thus first compared whether our algorithms produce AR-. CAR-. AAR-. and CAAR-values that are identical to those benchmarks that are created by alternative software solutions or are available in published research papers. 

    The below table shows the validation status of the EST expected return models:

    Expected return model Model validated?
    Market Model Yes, EST results match benchmark(s)
    Market Adjusted Yes, EST results match benchmark(s)
    Comparison Period Mean Adjusted Yes, EST results match benchmark(s)
    CAPM Yes, EST results match benchmark(s)
    Fama-French 3 Factor Model No benchmark has been found yet
    Fama-French-Momentum 4 Factor Model No benchmark has been found yet
    Fama-French 5 Factor Model No benchmark has been found yet

    The algorithms of the individual test statistics apply across the different expected factor-based return models. This means for the benchmarking that the algorithms can be considered as correctly designed once their outputs were found to match the benchmark(s) in one of the expected return models. To be sure, however, we programmed an internal service that compared all EST test statistics results per each model (except for the Fama French models) with the corresponding benchmark(s). 

    The below table shows the validation status of our test statistics (incl. p-values):

    Level(s) EST variable  Variable calculation validated?
    AR T-Value No benchmark has been found yet, but this is a simple t-value calculation with little room for error
    CAR T-Value No benchmark has been found yet, but this is a simple t-value calculation with little room for error
    AAR, CAAR Cross-Sectional T Yes, EST results match benchmark(s)
    AAR, CAAR CDA T Yes, EST results match benchmark(s)
    AAR, CAAR Patell Z Yes, EST results match benchmark(s)
    AAR, CAAR Adjusted Patell Z Yes, EST results match benchmark(s)
    AAR, CAAR Stand. Cross-Section. T Yes, EST results match benchmark(s)
    AAR, CAAR Adj. StdCSect T Yes, EST results match benchmark(s)
    AAR, CAAR Skewness Corrected T Yes, EST results match benchmark(s)
    AAR, CAAR Rank Z Yes, EST results match benchmark(s)
    AAR, CAAR Generalized Rank Z Yes, EST results match benchmark(s)
    AAR, CAAR Generalized Rank T Yes, EST results match benchmark(s)
    AAR, CAAR Sign Z Yes, EST results match benchmark(s)
    AAR Wilcoxon Yes, EST results match benchmark(s)

    Please further note: 
    - All validation was performed through a 1:1 comparison of results that were produced by EventStudyTools and the benchmark source. In case we compared against an alternative software, we used the EST ARC example dataset as a source for both the EST algorithms and the alternative software benchmark.
    - We will update this page as we progress in our search for benchmarks on the variables or expected return models that are not yet covered
    - In case you have questions on the benchmarking or want the data of a certain variable and its benchmark(s), please reach out to us.